高一年级数学下册(第2课时)《函数y=Asin(ωx+φ)的性质及应用》PPT教学课件










《高一年级数学下册(第2课时)《函数y=Asin(ωx+φ)的性质及应用》PPT教学课件》是由用户上传到老师板报网,类型是数学课件,大小为4.57 MB,总共有51页,格式为pptx。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。更多关于 数学课件 请在老师板报网直接搜索
函数y=Asin(ωx+φ)的图象第2课时 函数y=Asin(ωx+φ)的性质及应用第一章三角函数CONTENTS自主预习学案互动探究学案课时作业学案010203栏目导航自主预习学案第一章三角函数01在物理中,我们已经学习了简谐运动,了解其运动的规律及图象.那么如何用数学知识来研究它的性质呢?第一章三角函数往复运动一次所需要的时间1.函数y=Asin(ωx+φ),x∈[0,+∞)(其中A>0,ω>0)中各量的物理意义物理中,描述简谐运动的物理量,如振幅、周期和频率等都与函数y=Asin(ωx+φ)中的常数有关:(1)A:它表示做简谐运动的物体离开平衡位置的最大距离,称为振幅(amplitudeofvibration);(2)T:T=2πω,它表示做简谐运动的物体____________________________,称为周期(period);1.函数y=Asin(ωx+φ),x∈[0,+∞)(其中A>0,ω>0)中各量的物理意义物理中,描述简谐运动的物理量,如振幅、周期和频率等都与函数y=Asin(ωx+φ)中的常数有关:(1)A:它表示做简谐运动的物体离开平衡位置的最大距离,称为振幅(amplitudeofvibration);(2)T:T=2πω,它表示做简谐运动的物体____________________________,称为周期(period);第一章三角函数往复运动的次数(3)f:f=1T=ω2π,它表示做简谐运动的物体在单位时间内__________________,称为频率(frequency);(4)ωx+φ:称为相位(phase);(5)φ:__________________,称为初相(initialphase).知识延伸:当A<0或ω<0时,应先用诱导公式将三角函数符号前的数或x的系数化为正数,再确定初相φ.如函数y=-sin(2x-π3)的初相不是φ=-π3,∵A=-1<0,y=-sin(2x-π3)=sin[π+(2x-π3)]=sin(2x+2π3),∴初相φ=2π3.x=0时的相位(3)f:f=1T=ω2π,它表示做简谐运动的物体在单位时间内__________________,称为频率(frequency);(4)ωx+φ:称为相位(phase);(5)φ:__________________,称为初相(initialphase).知识延伸:当A<0或ω<0时,应先用诱导公式将三角函数符号前的数或x的系数化为正数,再确定初相φ.如函数y=-sin(2x-π3)的初相不是φ=-π3,∵A=-1<0,y=-sin(2x-π3)=sin[π+(2x-π3)]=sin(2x+2π3),∴初相φ=2π3.第一章三角函数R2.函数y=Asin(ωx+φ)(A>0,ω>0)的有关性质名称性质定义域______值域________________周期性T=______对称性对称中心(kπ-φω,0)(k∈Z)[-A,A]2πω2.函数y=Asin(ωx+φ)(A>0,ω>0)的有关性质名称性质定义域______值域________________周期性T=______对称性对称中心(kπ-φω,0)(k∈Z)2πω第一章三角函数对称轴x=kπω+π-2φ2ω(k∈Z)奇偶性当____________(k∈Z)时是奇函数当φ=kπ+π2(k∈Z)时是偶函数单调性由2kπ-π2≤ωx+φ≤2kπ+π2,k∈Z,解得单调递增区间由2kπ+π2≤2ωx+φ≤2kπ+3π2,k∈Z,解得单调递减区间φ=kπ对称轴x=kπω+π-2φ2ω(k∈Z)奇偶性当____________(k∈Z)时是奇函数当φ=kπ+π2(k∈Z)时是偶函数单调性由2kπ-π2≤ωx+φ≤2kπ+π2,k∈Z,解得单调递增区间由2kπ+π2≤2ωx+φ≤2kπ+3π2,k∈Z,解得单调递减区间φ=kπ√1.判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.(1)函数y=12sinx的图象是由函数y=2sinx的图象上所有点的纵坐标缩短为原来的14得到的.()(2)对函数y=Asin(ωx+φ)的图象进行变换时必须先平移变换再伸缩变换.()×1.判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.(1)函数y=12sinx的图象是由函数y=2sinx的图象上所有点的纵坐标缩短为原来的14得到的.()(2)对函数y=Asin(ωx+φ)的图象进行变换时必须先平移变换再伸缩变换.()第一章三角函数(3)将函数y=sin2x的图象向右平移π2个单位长度,所得图象对应的函数是偶函数.()(4)函数y=sin(2x+π3)的图象对称轴为x=kπ2+π12,k∈Z.()×√(3)将函数y=sin2x的图象向右平移π2个单位长度,所得图象对应的函数是偶函数.()(4)函数y=sin(2x+π3)的图象对称轴为x=kπ2+π12,k∈Z.()第一章三角函数2.函数y=3sinx2+π3的周期、振幅依次是()A.4π,3B.4π,-3C.π,3D.π,-33.简谐运动y=14sin13πx-π12的频率f=______.A[解析]周期T=2π13π=6,则频率f=1T=16.162.函数y=3sinx2+π3的周期、振幅依次是()A.4π,3B.4π,-3C.π,3D.π,-33.简谐运动y=14sin13πx-π12的频率f=______.[解析]周期T=2π13π=6,则频率f=1T=16.16第一章三角函数4.函数y=6sin3x-π8的最大值是()A.6B.7C.8D.18A4.函数y=6sin3x-π8的最大值是()A.6B.7C.8D.18互动探究学案第一章三角函数02如图所示是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象,试确定A,ω,φ的值.命题方向1 由图象求解析式⇨典例1第一章三角函数[解析]显然,这是函数在一个周期内的图象,我们所需要的信息都可在图中看出,因此要做的只是将图中信息与参数相联系.由于思考角度不一样,所以有三种解法.解法一:由图象可知振幅A=3,又T=5π6-(-π6)=π,∴ω=2πT=2ππ=2.由于点(-π6,0)在图象上,且为图象的第一个零点,因此令-π6×2+φ=0,得φ=π3.[解析]显然,这是函数在一个周期内的图象,我们所需要的信息都可在图中看出,因此要做的只是将图中信息与参数相联系.由于思考角度不一样,所以有三种解法.解法一:由图象可知振幅A=3,又T=5π6-(-π6)=π,∴ω=2πT=2ππ=2.由于点(-π6,0)在图象上,且为图象的第一个零点,因此令-π6×2+φ=0,得φ=π3.第一章三角函数解法二:由图象知振幅A=3,又图象过点(π3,0)和(5π6,0),根据“五点法”作图原理(以上两点可判为“五点法”中的第三点和第五点),得π3·ω+φ=π,5π6·ω+φ=2π.解得ω=2,φ=π3.解法二:由图象知振幅A=3,又图象过点(π3,0)和(5π6,0),根据“五点法”作图原理(以上两点可判为“五点法”中的第三点和第五点),得π3·ω+φ=π,5π6·ω+φ=2π.解得ω=2,φ=π3.第一章三角函数解法三:由图象可得A=3,又T=5π6-(-π6)=π,图象过点(-π6,0),可知图象由y=3sin2x向左平移π6个单位长度而得,∴y=3sin2(x+π6),即y=3sin(2x+π3).∴A=3,ω=2,φ=π3.解法三:由图象可得A=3,又T=5π6-(-π6)=π,图象过点(-π6,0),可知图象由y=3sin2x向左平移π6个单位长度而得,∴y=3sin2(x+π6),即y=3sin(2x+π3).∴A=3,ω=2,φ=π3.第一章三角函数『规律总结』由图象确立三角函数的解析式时,若设所求解析式为y=Asin(ωx+φ),则在观察图象的基础上可按以下规律来确定A,ω,φ.(1)A:一般可由图象上的最大值、最小值来确定.(2)ω:因为T=2πω,故往往通过求周期T来确定ω.可通过已知曲线与x轴的交点来确定T,即相邻的最高点与最低点之间的距离为T2;相邻的两个最高点(或最低点)之间的距离为T.『规律总结』由图象确立三角函数的解析式时,若设所求解析式为y=Asin(ωx+φ),则在观察图象的基础上可按以下规律来确定A,ω,φ.(1)A:一般可由图象上的最大值、最小值来确定.(2)ω:因为T=2πω,故往往通过求周期T来确定ω.可通过已知曲线与x轴的交点来确定T,即相邻的最高点与最低点之间的距离为T2;相邻的两个最高点(或最低点)之间的距离为T.第一章三角函数(3)φ:从“五点法”中的第一个点(-φω,0)(也叫初始点)作为突破口,要从图象的升降情况找准第一个点的位置.依据五点列表法原理,点的序号与式子的关系如下:“第一点”(即图象上升时与x轴的交点)为ωx+φ=0;“第二点”(即图象曲线的“峰点”)为ωx+φ=π2;“第三点”(即图象下降时与x轴的交点)为ωx+φ=π;(3)φ:从“五点法”中的第一个点(-φω,0)(也叫初始点)作为突破口,要从图象的升降情况找准第一个点的位置.依据五点列表法原理,点的序号与式子的关系如下:“第一点”(即图象上升时与x轴的交点)为ωx+φ=0;“第二点”(即图象曲线的“峰点”)为ωx+φ=π2;“第三点”(即图象下降时与x轴的交点)为ωx+φ=π;第一章三角函数“第四点”(即图象曲线的“谷点”)为ωx+φ=3π2;“第五点”(即图象第二次上升时与x轴的交点)为ωx+φ=2π.在用以上方法确定φ的值时,还要注意题目中给出的φ的范围,不在要求范围内的要通过周期性转化到要求范围内.(4)A,ω,φ三个量中初相φ的确定是一个难点,除使用初始点(-φω,0)外,还可在五点中找两个特殊点列方程组来求解φ.,“第四点”(即图象曲线的“谷点”)为ωx+φ=3π2;“第五点”(即图象第二次上升时与x轴的交点)为ωx+φ=2π.在用以上方法确定φ的值时,还要注意题目中给出的φ的范围,不在要求范围内的要通过周期性转化到要求范围内.(4)A,ω,φ三个量中初相φ的确定是一个难点,除使用初始点(-φω,0)外,还可在五点中找两个特殊点列方程组来求解φ.,第一章三角函数〔跟踪练习1〕如图为y=Asin(ωx+φ)(A>0,ω>0,|φ|≤π2)图象的一段,试确定此函数解析式.〔跟踪练习1〕如图为y=Asin(ωx+φ)(A>0,ω>0,|φ|≤π2)图象的一段,试确定此函数解析式.第一章三角函数[解析]该函数的周期T=13π3-π3=4π,∴ω=2πT=12.又∵函数的最大值为3,故A=3.∴y=3sin(12x+φ).法一:所给图象是由函数y=3sinx2向右平移π3个单位长度得到的,于是所求解析式为y=3sin[12(x-π3)],即y=3sin(12x-π6).[解析]该函数的周期T=13π3-π3=4π,∴ω=2πT=12.又∵函数的最大值为3,故A=3.∴y=3sin(12x+φ).法一:所给图象是由函数y=3sinx2向右平移π3个单位长度得到的,于是所求解析式为y=3sin[12(x-π3)],即y=3sin(12x-π6).第一章三角函数法二:∵周期为4π,∴由图象知最大值点为(4π3,3).∴3sin(12×4π3+φ)=3.∴2π3+φ=2kπ+π2,k∈Z.∴φ=2kπ-π6,k∈Z.∵|φ|≤π2,∴φ=-π6.∴所求解析式为y=3sin(12x-π6).法二:∵周期为4π,∴由图象知最大值点为(4π3,3).∴3sin(12×4π3+φ)=3.∴2π3+φ=2kπ+π2,k∈Z.∴φ=2kπ-π6,k∈Z.∵|φ|≤π2,∴φ=-π6.∴所求解析式为y=3sin(12x-π6).第一章三角函数法三:∵图象过点(0,-32),∴3sinφ=-32.∴sinφ=-12.又∵-π2≤φ≤π2,∴φ=-π6.∴所求解析式为y=3sin(12x-π6).法三:∵图象过点(0,-32),∴3sinφ=-32.∴sinφ=-12.又∵-π2≤φ≤π2,∴φ=-π6.∴所求解析式为y=3sin(12x-π6).第一章三角函数法四:由图象过点(π3,0),且该点在递增区间上,∴12×π3+φ=2kπ,k∈Z,∴φ=2kπ-π6,k∈Z.∵|φ|≤π2,∴φ=-π6.∴所求解析式为y=3sin(12x-π6).法四:由图象过点(π3,0),且该点在递增区间上,∴12×π3+φ=2kπ,k∈Z,∴φ=2kπ-π6,k∈Z.∵|φ|≤π2,∴φ=-π6.∴所求解析式为y=3sin(12x-π6).第一章三角函数命题方向2 函数⇨y=Asin(ωx+φ)图象的对称性典例2已知函数f(x)=sin(ωx+π3)(ω>0)的最小正周期为π,则该函数图象()A.关于点(π3,0)对称B.关于直线x=π4对称C.关于点(π4,0)对称D.关于直线x=π3对称A已知函数f(x)=sin(ωx+π3)(ω>0)的最小正周期为π,则该函数图象()A.关于点(π3,0)对称B.关于直线x=π4对称C.关于点(π4,0)对称D.关于直线x=π3对称第一章三角函数[思路分析]求参数ω→得函数fx的解析式→由ωx+π3=kπ+π2k∈Z得对称轴→由ωx+π3=kπk∈Z得对称中心→选出正确选项[思路分析]求参数ω→得函数fx的解析式→由ωx+π3=kπ+π2k∈Z得对称轴→由ωx+π3=kπk∈Z得对称中心→选出正确选项第一章三角函数[解析]由T=2πω=π,解得ω=2,则f(x)=sin(2x+π3),令2x+π3=kπ+π2,k∈Z,得x=kπ2+π12,k∈Z,即对称轴为x=kπ2+π12,k∈Z.令2x+π3=kπ,k∈Z,得x=kπ2-π6,k∈Z,即对称中心为(kπ2-π6,0),k∈Z.从而可判断A正确.[解析]由T=2πω=π,解得ω=2,则f(x)=sin(2x+π3),令2x+π3=kπ+π2,k∈Z,得x=kπ2+π12,k∈Z,即对称轴为x=kπ2+π12,k∈Z.令2x+π3=kπ,k∈Z,得x=kπ2-π6,k∈Z,即对称中心为(kπ2-π6,0),k∈Z.从而可判断A正确.第一章三角函数『规律总结』1.函数y=Asin(ωx+φ)的对称轴方程由ωx+φ=kπ+π2,k∈Z求得,即x=kπ+π2-φω,k∈Z;对称中心由ωx+φ=kπ,k∈Z求得,即得kπ-φω,0,k∈Z.2.函数y=Acos(ωx+φ)的对称轴方程由ωx+φ=kπ,k∈Z求得,即x=kπ-φω,k∈Z,对称中心由ωx+φ=kπ+π2,k∈Z求得,即为(kπ+π2-φω,0),k∈Z.『规律总结』1.函数y=Asin(ωx+φ)的对称轴方程由ωx+φ=kπ+π2,k∈Z求得,即x=kπ+π2-φω,k∈Z;对称中心由ωx+φ=kπ,k∈Z求得,即得kπ-φω,0,k∈Z.2.函数y=Acos(ωx+φ)的对称轴方程由ωx+φ=kπ,k∈Z求得,即x=kπ-φω,k∈Z,对称中心由ωx+φ=kπ+π2,k∈Z求得,即为(kπ+π2-φω,0),k∈Z.第一章三角函数〔跟踪练习2〕下列四个函数中,同时具有:①最小正周期是π,②图象关于x=π3对称的是()A.y=sin(x2+π6)B.y=sin(2x+π6)C.y=sin(2x-π3)D.y=sin(2x-π6)D〔跟踪练习2〕下列四个函数中,同时具有:①最小正周期是π,②图象关于x=π3对称的是()A.y=sin(x2+π6)B.y=sin(2x+π6)C.y=sin(2x-π3)D.y=sin(2x-π6)设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线x=π8.(1)求φ;(2)求函数y=f(x)的单调区间及最值;(3)画出函数y=f(x)在区间[0,π]上的图象.函数y=Asin(ωx+φ)性质的综合应用典例3设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线x=π8.(1)求φ;(2)求函数y=f(x)的单调区间及最值;(3)画出函数y=f(x)在区间[0,π]上的图象.第一章三角函数[思路分析]本题关键是对图象的对称轴为x=π8这一条件的利用,由图象一对称轴为x=π8得:当x=π8时2x+φ=kπ+π2(k∈Z)进而可求φ值.[解析](1)由2x+φ=kπ+π2,k∈Z得x=kπ2+π4-φ2,令kπ2+π4-φ2=π8,解得φ=kπ+π4,k∈Z.∵-π<φ<0,∴φ=-3π4.[思路分析]本题关键是对图象的对称轴为x=π8这一条件的利用,由图象一对称轴为x=π8得:当x=π8时2x+φ=kπ+π2(k∈Z)进而可求φ值.[解析](1)由2x+φ=kπ+π2,k∈Z得x=kπ2+π4-φ2,令kπ2+π4-φ2=π8,解得φ=kπ+π4,k∈Z.∵-π<φ<0,∴φ=-3π4.第一章三角函数(2)由(1)知,f(x)=sin(2x-3π4),由2kπ-π2≤2x-3π4≤2kπ+π2(k∈Z),解得kπ+π8≤x≤kπ+5π8(k∈Z),故函数的单调递增区间是[kπ+π8,kπ+5π8](k∈Z).同理可得函数的单调递减区间是[kπ+5π8,kπ+9π8](k∈Z).当2x-3π4=2kπ+π2(k∈Z),即x=kπ+5π8(k∈Z)时函数有最大值1;当2x-3π4=2kπ-π2(k∈Z),即x=kπ+π8(k∈Z)时函数有最小值-1.(2)由(1)知,f(x)=sin(2x-3π4),由2kπ-π2≤2x-3π4≤2kπ+π2(k∈Z),解得kπ+π8≤x≤kπ+5π8(k∈Z),故函数的单调递增区间是[kπ+π8,kπ+5π8](k∈Z).同理可得函数的单调递减区间是[kπ+5π8,kπ+9π8](k∈Z).当2x-3π4=2kπ+π2(k∈Z),即x=kπ+5π8(k∈Z)时函数有最大值1;当2x-3π4=2kπ-π2(k∈Z),即x=kπ+π8(k∈Z)时函数有最小值-1.第一章三角函数(3)由y=sin(2x-3π4)知,x0π83π85π87π8π2x-3π4-3π4-π20π2π5π4y-22-1010-22(3)由y=sin(2x-3π4)知,x0π83π85π87π8π2x-3π4-3π4-π20π2π5π4y-22-1010-22第一章三角函数故函数y=f(x)在区间[0,π]上的图象是故函数y=f(x)在区间[0,π]上的图象是第一章三角函数〔跟踪练习3〕已知函数f(x)=2sin(π6-2x)+a.(1)求函数f(x)的最小正周期;(2)求函数f(x)的单调递减区间;(3)若x∈[0,π2]时,f(x)的最小值为-2,求a的值.〔跟踪练习3〕已知函数f(x)=2sin(π6-2x)+a.(1)求函数f(x)的最小正周期;(2)求函数f(x)的单调递减区间;(3)若x∈[0,π2]时,f(x)的最小值为-2,求a的值.第一章三角函数[解析](1)易知T=2π|-2|=π.(2)f(x)=2sin(π6-2x)+a=2sin(2x+5π6)+a.由2kπ+π2≤2x+5π6≤2kπ+3π2(k∈Z).得kπ-π6≤x≤kπ+π3(k∈Z).所以f(x)的单调递减区间为[kπ-π6,kπ+π3](k∈Z).(3)由0≤x≤π2,得5π6≤2x+5π6≤11π6,所以f(x)的最小值为-2+a=-2.所以a=0.[解析](1)易知T=2π|-2|=π.(2)f(x)=2sin(π6-2x)+a=2sin(2x+5π6)+a.由2kπ+π2≤2x+5π6≤2kπ+3π2(k∈Z).得kπ-π6≤x≤kπ+π3(k∈Z).所以f(x)的单调递减区间为[kπ-π6,kπ+π3](k∈Z).(3)由0≤x≤π2,得5π6≤2x+5π6≤11π6,所以f(x)的最小值为-2+a=-2.所以a=0.函数y=2sin(-2x+π3)的相位和初相分别是()A.-2x+π3,π3B.2x-π3,-π3C.2x+2π3,2π3D.2x+2π3,π3相位、初相概念理解错误典例4函数y=2sin(-2x+π3)的相位和初相分别是()A.-2x+π3,π3B.2x-π3,-π3C.2x+2π3,2π3D.2x+2π3,π3第一章三角函数[错解]对解答本题时易犯的错误具体分析如下:常见错误错误原因相位和初相分别是-2x+π3,π3错解均忽视了相位和初相的概念:概念中要求A>0,ω>0.当不满足条件时应设法创造出条件.y=2sin(-2x+π3)=-2sin(2x-π3)∴相位和初相分别是2x-π3,-π3[错解]对解答本题时易犯的错误具体分析如下:常见错误错误原因相位和初相分别是-2x+π3,π3错解均忽视了相位和初相的概念:概念中要求A>0,ω>0.当不满足条件时应设法创造出条件.y=2sin(-2x+π3)=-2sin(2x-π3)∴相位和初相分别是2x-π3,-π3第一章三角函数[错因分析] 此类问题一定要注意满足定义中的前提条件是“A>0,ω>0”,若不满足,则必须先利用诱导公式转换为“A>0,ω>0”再求.[正解]C∵y=2sin(-2x+π3)=2sin[π-(-2x+π3)]=2sin(2x+2π3)∴相位和初相分别是2x+2π3,2π3.[误区警示]要正确理解函数y=Asin(ωx+φ)中A、ω、φ的意义.[正解]C∵y=2sin(-2x+π3)=2sin[π-(-2x+π3)]=2sin(2x+2π3)∴相位和初相分别是2x+2π3,2π3.[误区警示]要正确理解函数y=Asin(ωx+φ)中A、ω、φ的意义.第一章三角函数〔跟踪练习4〕已知简谐运动f(x)=2sin(π3x+φ)(|φ|<π2)的图象经过点(0,1),则该简谐运动的最小正周期T和初相φ分别为()A.T=6,φ=π6B.T=6,φ=π3C.T=6π,φ=π6D.T=6π,φ=π3A〔跟踪练习4〕已知简谐运动f(x)=2sin(π3x+φ)(|φ|<π2)的图象经过点(0,1),则该简谐运动的最小正周期T和初相φ分别为()A.T=6,φ=π6B.T=6,φ=π3C.T=6π,φ=π6D.T=6π,φ=π3第一章三角函数[解析]∵T=2πω=2ππ3=6,又图象过(0,1)点,∴sinφ=12.∵-π2<φ<π2,∴φ=π6.[解析]∵T=2πω=2ππ3=6,又图象过(0,1)点,∴sinφ=12.∵-π2<φ<π2,∴φ=π6.1.已知函数y=Asin(ωx+φ)(A>0,ω>0)的振幅为12,周期为2π3,初相为π6,则该函数的表达式为()A.y=12sin(x3+π6)B.y=12sin(x3-π6)C.y=12sin(3x+π6)D.y=12sin(3x-π6)C1.已知函数y=Asin(ωx+φ)(A>0,ω>0)的振幅为12,周期为2π3,初相为π6,则该函数的表达式为()A.y=12sin(x3+π6)B.y=12sin(x3-π6)C.y=12sin(3x+π6)D.y=12sin(3x-π6)第一章三角函数2.函数y=cos(2x-π6)+1的一个对称中心为()A.(π6,0)B.(π3,0)C.(π6,1)D.(π3,1)D2.函数y=cos(2x-π6)+1的一个对称中心为()A.(π6,0)B.(π3,0)C.(π6,1)D.(π3,1)第一章三角函数3.(全国卷Ⅱ)函数y=Asin(ωx+φ)的部分图象如图所示,则()A.y=2sin(2x-π6)B.y=2sin(2x-π3)C.y=2sin(x+π6)D.y=2sin(x+π3)A3.(全国卷Ⅱ)函数y=Asin(ωx+φ)的部分图象如图所示,则()A.y=2sin(2x-π6)B.y=2sin(2x-π3)C.y=2sin(x+π6)D.y=2sin(x+π3)第一章三角函数[解析]由图易知A=2,因为周期T满足T2=π3-(-π6),所以T=π,ω=2πT=2.由x=π3时,y=2可知2×π3+φ=π2+2kπ(k∈Z),所以φ=-π6+2kπ(k∈Z),结合选项可知函数解析式为y=2sin(2x-π6).[解析]由图易知A=2,因为周期T满足T2=π3-(-π6),所以T=π,ω=2πT=2.由x=π3时,y=2可知2×π3+φ=π2+2kπ(k∈Z),所以φ=-π6+2kπ(k∈Z),结合选项可知函数解析式为y=2sin(2x-π6).第一章三角函数4.已知ω>0,0<φ<π,直线x=π4和x=5π4是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,则φ=()A.π4B.π3C.π2D.3π4A[解析]因为直线x=π4和x=5π4是函数f(x)的图象中的两条相邻的对称轴,所以5π4-π4=T2,即T2=π,解得T=2π.又T=2πω=2π,所以ω=1.4.已知ω>0,0<φ<π,直线x=π4和x=5π4是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,则φ=()A.π4B.π3C.π2D.3π4[解析]因为直线x=π4和x=5π4是函数f(x)的图象中的两条相邻的对称轴,所以5π4-π4=T2,即T2=π,解得T=2π.又T=2πω=2π,所以ω=1.第一章三角函数所以f(x)=sin(x+φ).因为直线x=π4是函数f(x)的对称轴,所以π4+φ=π2+kπ(k∈Z),所以φ=π4+kπ(k∈Z).又0<φ<π,所以φ=π4.经检验知此时直线x=5π4也为函数f(x)的对称轴,所以选A.所以f(x)=sin(x+φ).因为直线x=π4是函数f(x)的对称轴,所以π4+φ=π2+kπ(k∈Z),所以φ=π4+kπ(k∈Z).又0<φ<π,所以φ=π4.经检验知此时直线x=5π4也为函数f(x)的对称轴,所以选A.第一章三角函数5.函数y=sinωx(ω>0)在区间[0,1]上恰好有50个最大值,则ω的取值范围是______________.[解析]T=2πω为其最小正周期,则(49+14)T≤1<(50+14)T时,有50个最大值点,所以ω∈[197π2,201π2).[197π2,201π2)[解析]T=2πω为其最小正周期,则(49+14)T≤1<(50+14)T时,有50个最大值点,所以ω∈[197π2,201π2).[197π2,201π2)课时作业学案第一章三角函数03谢谢观看数学必修④·人教A版新课标导学
-

八年级数学下册《探索勾股定理(1)》教学课件PPT下载
-

三年级数学下册《讲故事教学》课件PPT下载
-

人教版初中数学六年级上册第六单元《成反比例的量》课件
-

人教版初中数学六年级上册《第3课 成正比例的量》课件PPT下载
-

七年级初中数学《不等式的解集》参考课件PPT下载
-

青岛版二年级数学上册第四单元《乘法口诀》PPT课件下载
-
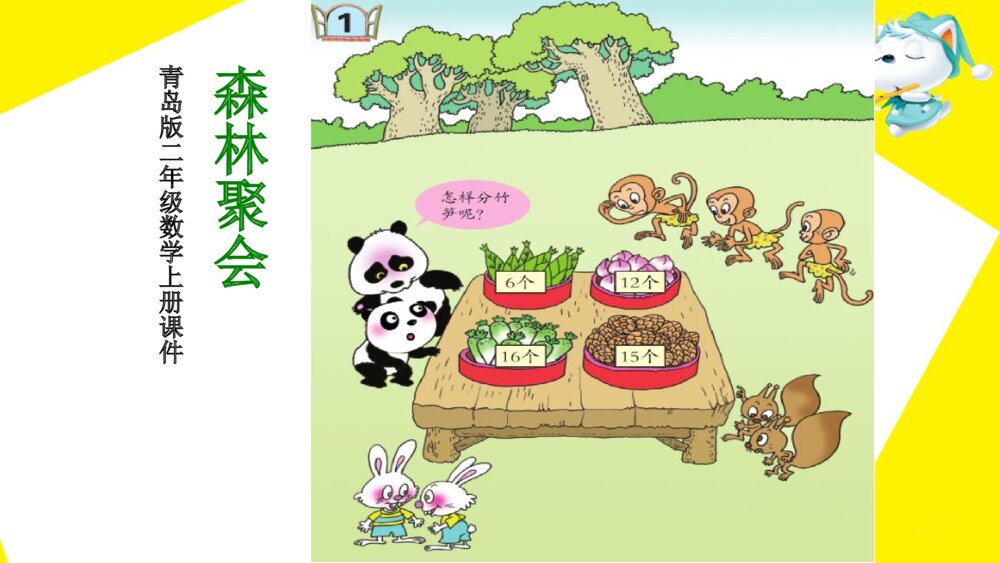
青岛版二年级数学上册·第五单元窗1_除法的初步认识·好PPT课件下载
-

七年级数学下册《不等式及其解集》参考课件PPT下载
-

冀教版·九年级数学上册《24.4 一元二次方程的应用--读一读 方程的近似解》教学PPT课件
-

华师大版初中数学八年级上册《因式分解平方差公式法》课件PPT下载
-

二年级数学下册《除法的初步认识》教学PPT课件下载
-

二年级数学上册·第五单元森林里的故事_除法的初步认识·平均分》教学PPT课件





































 赣公网安备 36010802000481号
赣公网安备 36010802000481号