高二年级数学上册(第1.1.2课时)《余弦定理》PPT教学课件










《高二年级数学上册(第1.1.2课时)《余弦定理》PPT教学课件》是由用户上传到老师板报网,类型是数学课件,大小为801.87 KB,总共有29页,格式为pptx。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。更多关于 数学课件 请在老师板报网直接搜索
主讲人:XXX第一章解三角形1.1.2余弦定理正弦定理和余弦定理目录CONTENS学习目标LEARNINGOBJECTIVES011.掌握余弦定理及其推论.(重点).2.掌握正、余弦定理的综合应用.(重点).3.能应用余弦定理判断三角形的形状.(易错点)01学习目标LEARNINGOBJECTIVES学习目标LEARNINGOBJECTIVES1.余弦定理文字表述三角形中任何一边的平方等于减去这两边与它们的的两倍公式表达a2=,b2=,c2=变形cosA=;cosB=a2+c2-b22ac;cosC=.a2+c2-2accosBa2+b2-2abcosCb2+c2-2bccosA其它两边的平方的和夹角的余弦的积b2+c2-a22bca2+b2-c22ab1.余弦定理文字表述三角形中任何一边的平方等于减去这两边与它们的的两倍公式表达a2=,b2=,c2=变形cosA=;cosB=a2+c2-b22ac;cosC=.b2+c2-a22bca2+b2-c22ab学习目标LEARNINGOBJECTIVES思考:在△ABC中,若a2
-

八年级数学下册《探索勾股定理(1)》教学课件PPT下载
-

三年级数学下册《讲故事教学》课件PPT下载
-

人教版初中数学六年级上册第六单元《成反比例的量》课件
-

人教版初中数学六年级上册《第3课 成正比例的量》课件PPT下载
-

七年级初中数学《不等式的解集》参考课件PPT下载
-

青岛版二年级数学上册第四单元《乘法口诀》PPT课件下载
-
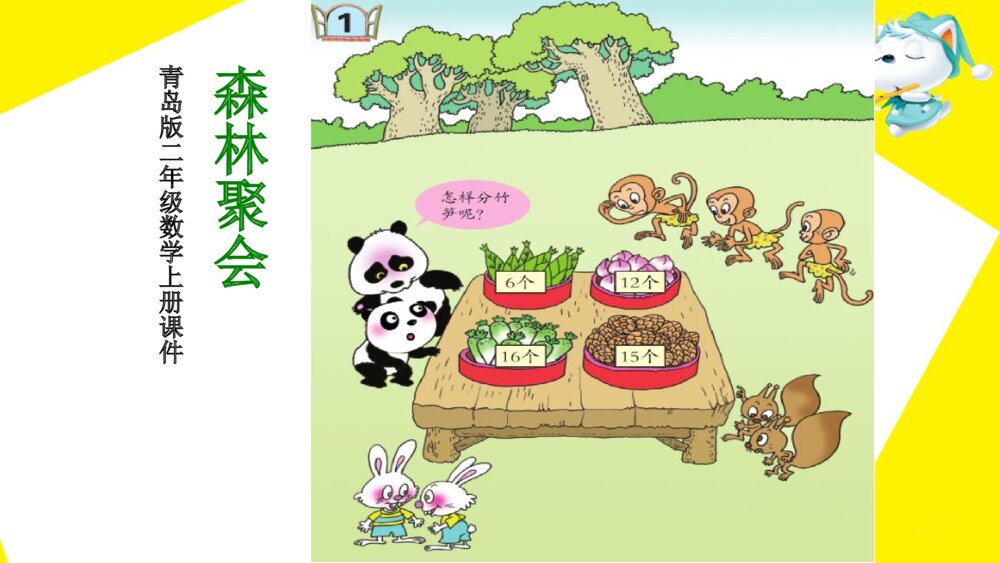
青岛版二年级数学上册·第五单元窗1_除法的初步认识·好PPT课件下载
-

七年级数学下册《不等式及其解集》参考课件PPT下载
-

冀教版·九年级数学上册《24.4 一元二次方程的应用--读一读 方程的近似解》教学PPT课件
-

华师大版初中数学八年级上册《因式分解平方差公式法》课件PPT下载
-

二年级数学下册《除法的初步认识》教学PPT课件下载
-

二年级数学上册·第五单元森林里的故事_除法的初步认识·平均分》教学PPT课件





































 赣公网安备 36010802000481号
赣公网安备 36010802000481号